NeuralFIM

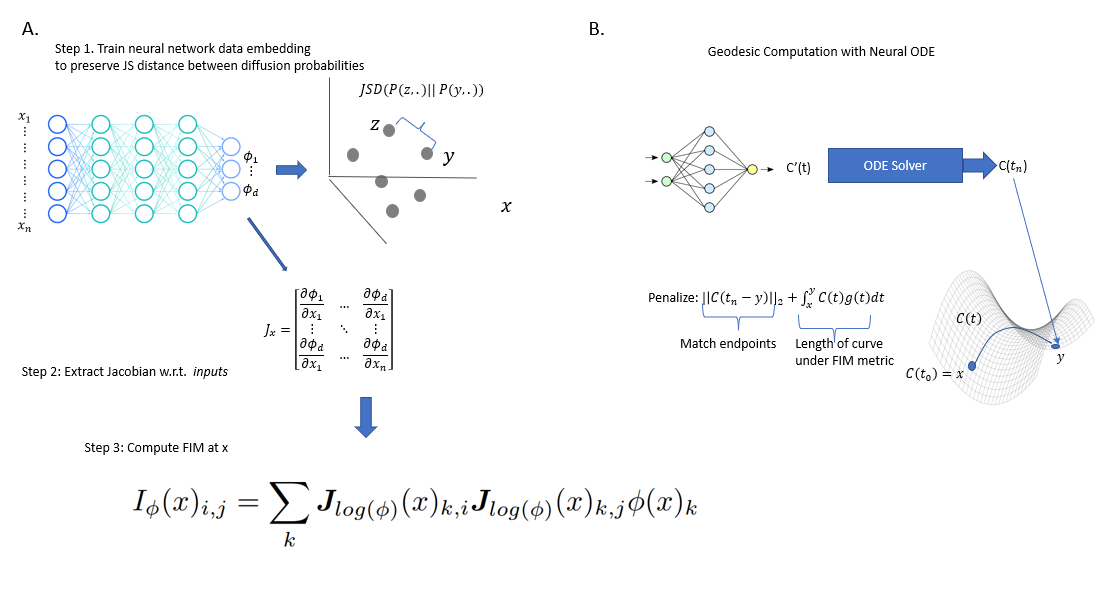
We propose neural FIM, a method for computing the Fisher information metric (FIM) from point cloud data. In order to apply this to data, we compute a data diffusion operator, which involves creating a data affinity matrix and then normalizing into a Markovian diffusion operator. We train a neural network embedding of the data that maintains Jensen--Shannon distances (JSD) between these distributions. Our network's output layer Jacobian with respect to the primary inputs is then used to construct the FIM. We show that since infinitesimal JS distances converge in theory to the FIM, our FIM converges to the true FIM on the data manifold. We also note that this connects neural FIM and the dimensionality reduction method PHATE with JSD rather than M-divergences, i.e. JSD-PHATE is a discretized version of neural FIM. Neural FIM creates an extensible metric space from discrete point cloud data such that information from the metric can inform us of manifold characteristics such as volume and geodesics. We showcase results on toy datasets as well as two single cell datasets of IPSC reprogramming and PBMCs (immune cells). In both cases we show that the FIM contains information pertaining to local volume illuminating branching points and cluster centers. We also show a use case for FIM in selecting parameters for the PHATE visualization method