Projects
- NeuralFIM (Neural Fisher Information Metric) a network that imbues point cloud data with smooth manifold-intrinsic geometric entities on high-dimensional data with fisher information metrics. Also has connections to JSD-PHATE and other desirable information theoretic quantities.
- Diffusion Curvature a method for computing diffusion-based curvature on high-dimensional data that hinges on the canonical data diffusion framework. Allows for estimation of neural network Hessians as well as curvature-based inference on point cloud data such as single-cell data.
- MIOFlow (Manifold Interpolating Optimal-Transport Flows for Trajectory Inference) a neural ODE to interpolates between static population snapshots, penalized by optimal transport with manifold ground distance. MIOFlow has theoretical links with dynamic optimal transport.
- MSPHATE (Multiscale PHATE) Capturing meaningful biological signals in high-dimensional data using a continuous coarse-graining process which can be used to produce both a high-level summarization and more detailed representations of the data.
- UDEMD (Embedding Signals on Knowledge Graphs with Unbalanced Diffusion Earth Mover's Distance) a fast multi-scale approximation of the Earth Mover's Distance with manifold geodesics as a ground distance between distributions on a manifold.
- MELD (Manifold Enhancement of Latent Dimensions) a graph signal processing tool to analyze multiple scRNA-seq samples from two or more conditions.
- Integrated Diffusion Combining multi-modal datasets by learning an integrated diffusion operator to effectively visualize the relationships between them.
- DEMD (Diffusion Earth Mover's Distance and Distribution Embeddings) a fast multi-scale approximation of the Earth Mover's Distance with manifold geodesics as a ground distance between distributions on a manifold.
- GSAE (Geometric Scattering Autoencoder) Here we combine the flexibility of deep learning with the representational power of graph scattering transforms to study thermodynamic landscapes within RNA folding.
- PhEMD (Phenotypic Earth Mover's Distance) a computational method to quantify relationships between drug perturbations on dozens to hundreds of single cell samples.
- Topological fMRI Analysis A novel fMRI analysis method based on the concepts of cubical persistent homology, which analyzes functions on structured data sets at different scales.
- TrajectoryNet Relates continuous normalizing flows with the Breiner formulation of dynamic optimal transport to perform continuous optimal transport in high dimensions in the neural network framework. Uses dynamic optimal transport to infer continuous cell trajectories over time.
- SAUCIE (Sparse AutoEncoders for Clustering Imputation and Embedding) a deep autoencoder architecture that allows for unsupervised exploration of data, and has novel regularizations that allow for data denoising, batch normalization, clustering and visualization simultaneously in various layers of the network.
- PHATE (Potential of Heat-diffusion Affinity-based Transition Embedding) a visualization and dimensionality reduction technique that is sensitive to local and global relationships and successfully preserves structures of interest in biological data including cluster structure and branching trajectory structure.
- MAGAN (Manifold Alignment Generative Adversarial Network) a dual GAN (generative adversarial network) framework that can find correspondences between two data modalities measuring the same system to create an integrated dataset
- Neuron Editing a neural network inference method which maps between datasets with the signal learned on a subset of the data, for example when a drug perturbation is applied to one cell type neuron editing can be used to apply it in silico to another cell type.
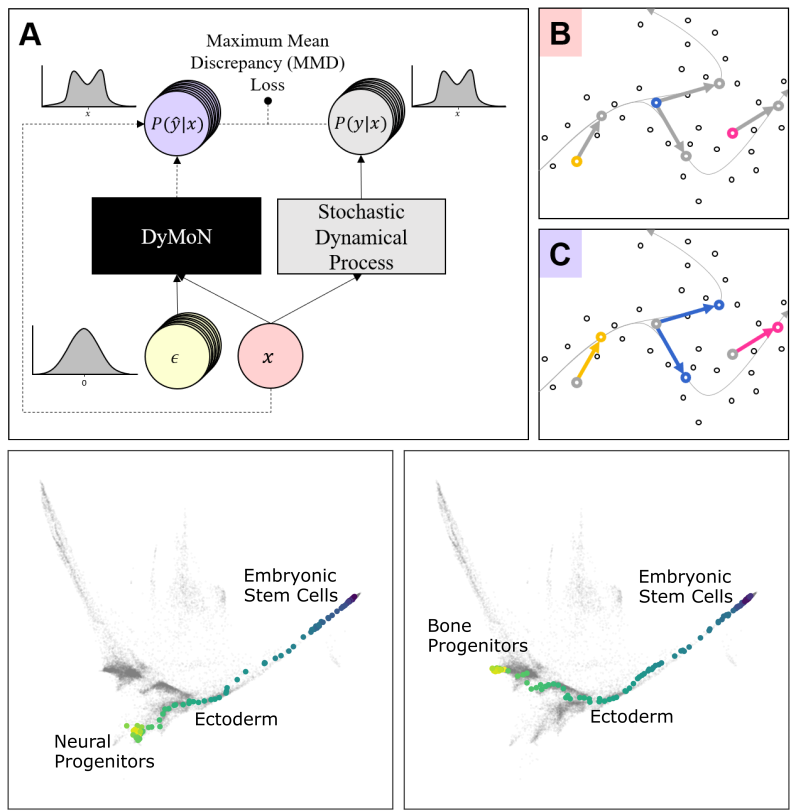
- DyMoN (Dynamics Modeling Networks) A neural network framework for learning stochastic dynamics for generative and embedding purposes. DyMoN serves as a deep model that itself embodies a dynamic system such that the gene logic and features driving the system can be studied.
- MAGIC (Markov Affinity-based Graph Imputation of Cells) an algorithm that uses graph signal processing for denoising and missing transcript recovery in single cell RNA sequencing. MAGIC successfully recovers gene-gene relationships from data and allows for the prediction of transcription targets.
- TIDES (Trajectory Interpolated DREMI Scores) Learning time-varying information flow form single-cell epithelial to mesenchymal transition data
- SUGAR (Synthesis Using Geometrically Aligned Random-walks) A new kind of data generation algorithm that generates of data geometry rather than density and is able to generate data in sparse regions and predicts hypothetical data points.
- DREMI (conditional Density-based Resampled Estimate of Mutual Information) a computational method based on established statistical concepts, to characterize signaling network relationships by quantifying the strengths of network edges and deriving signaling response functions.
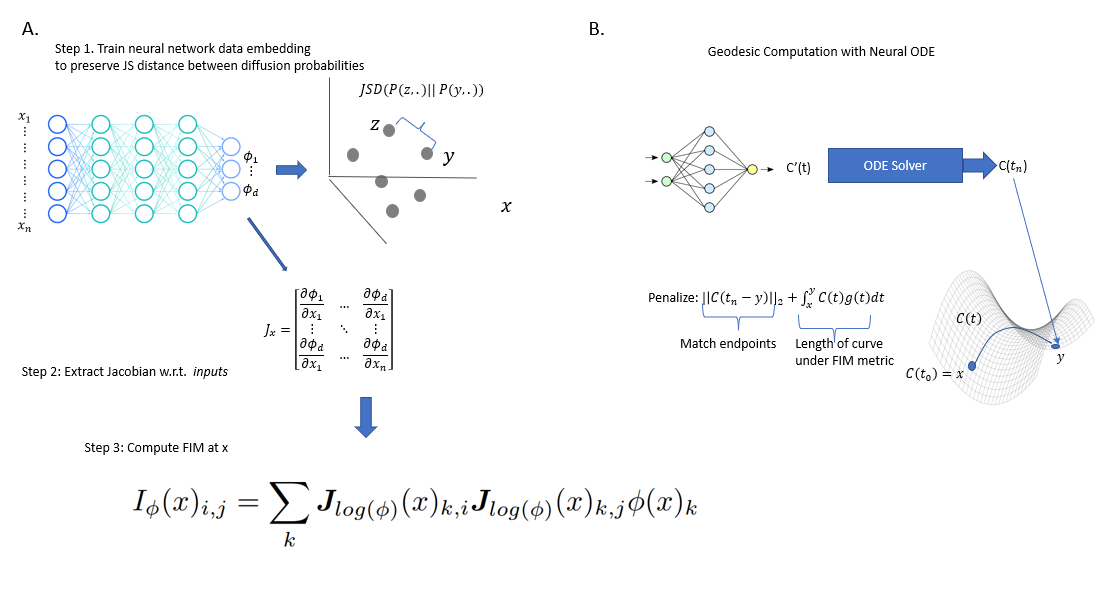
NeuralFIM
point cloud data with smooth manifold-intrinsic geometric entities
We propose neural FIM, a method for computing the Fisher information metric (FIM) from point cloud data. In order to apply this to data, we compute a data diffusion operator, which involves creating a data affinity matrix and then normalizing into a Markovian diffusion operator. We train a neural network embedding of the data that maintains Jensen--Shannon distances (JSD) between these distributions. Our network's output layer Jacobian with respect to the primary inputs is then used to construct the FIM. We show that since infinitesimal JS distances converge in theory to the FIM, our FIM converges to the true FIM on the data manifold. We also note that this connects neural FIM and the dimensionality reduction method PHATE with JSD rather than M-divergences, i.e. JSD-PHATE is a discretized version of neural FIM. Neural FIM creates an extensible metric space from discrete point cloud data such that information from the metric can inform us of manifold characteristics such as volume and geodesics. We showcase results on toy datasets as well as two single cell datasets of IPSC reprogramming and PBMCs (immune cells). In both cases we show that the FIM contains information pertaining to local volume illuminating branching points and cluster centers. We also show a use case for FIM in selecting parameters for the PHATE visualization method
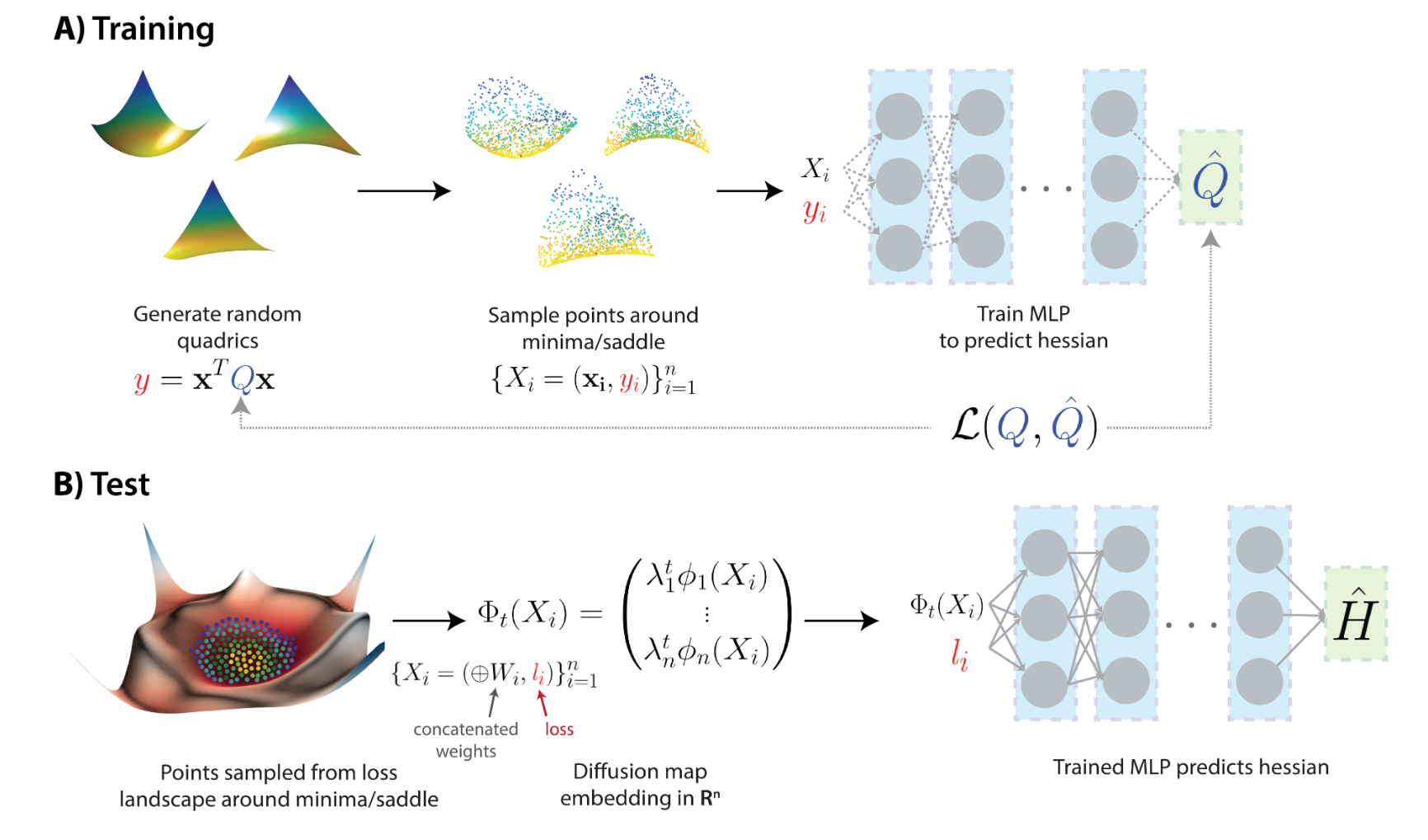
Diffusion Curvature
Estimating Local Curvature in High Dimensional Data
We introduce a new intrinsic measure of local curvature on point-cloud data called diffusion curvature. Our measure uses the framework of diffusion maps, including the data diffusion operator, to structure point cloud data and define local curvature based on the laziness of a random walk starting at a point or region of the data. We show that this laziness directly relates to volume comparison results from Riemannian geometry. We then extend this scalar curvature notion to an entire quadratic form using neural network estimations based on the diffusion map of point-cloud data. We show applications of both estimations on toy data, single-cell data and on estimating local Hessian matrices of neural network loss landscapes.
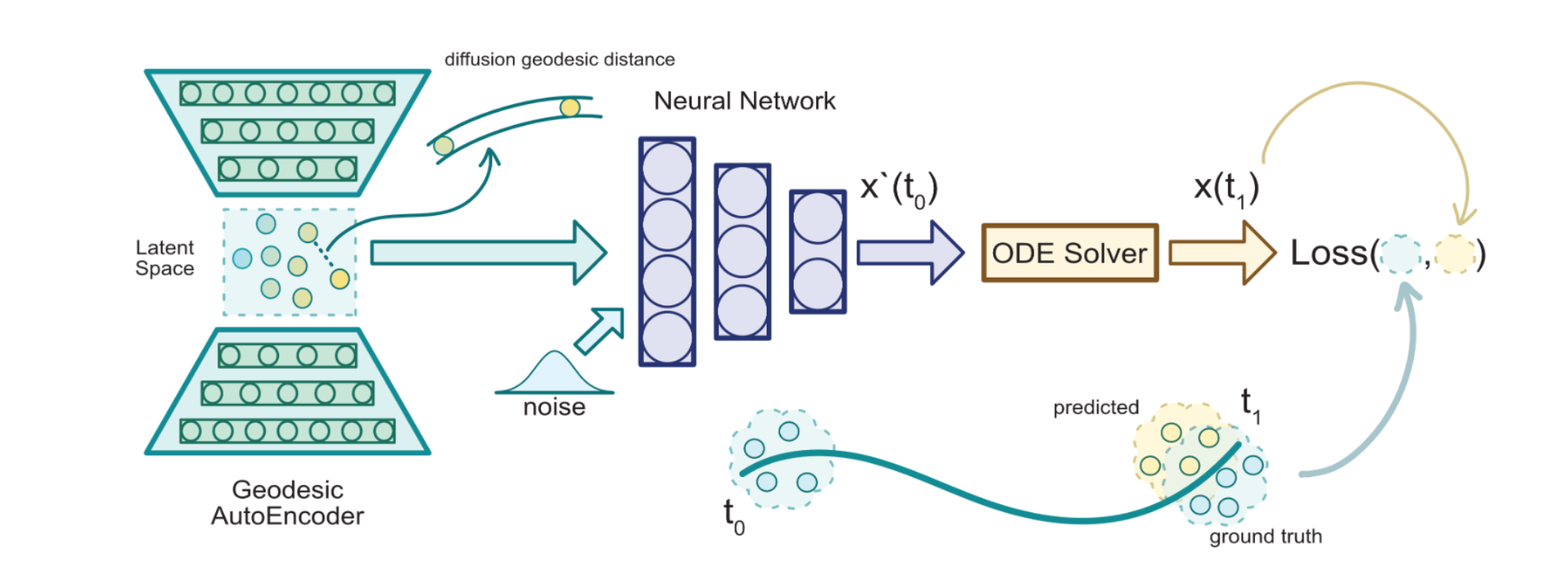
MIOFlow
Continuous Population Dynamics from Static Snapshots
We present a method called Manifold Interpolating Optimal-Transport Flow (MIOFlow) that learns stochastic, continuous population dynamics from static snapshot samples taken at sporadic timepoints. MIOFlow combines dynamic models, manifold learning, and optimal transport by training neural ordinary differential equations (Neural ODE) to interpolate between static population snapshots as penalized by optimal transport with manifold ground distance. Further, we ensure that the flow follows the geometry by operating in the latent space of an autoencoder that we call a geodesic autoencoder (GAE). In GAE the latent space distance between points is regularized to match a novel multiscale geodesic distance on the data manifold that we define. We show that this method is superior to normalizing flows, Schrödinger bridges and other generative models that are designed to flow from noise to data in terms of interpolating between populations. Theoretically, we link these trajectories with dynamic optimal transport. We evaluate our method on simulated data with bifurcations and merges, as well as scRNA-seq data from embryoid body differentiation, and acute myeloid leukemia treatment.
MSPHATE
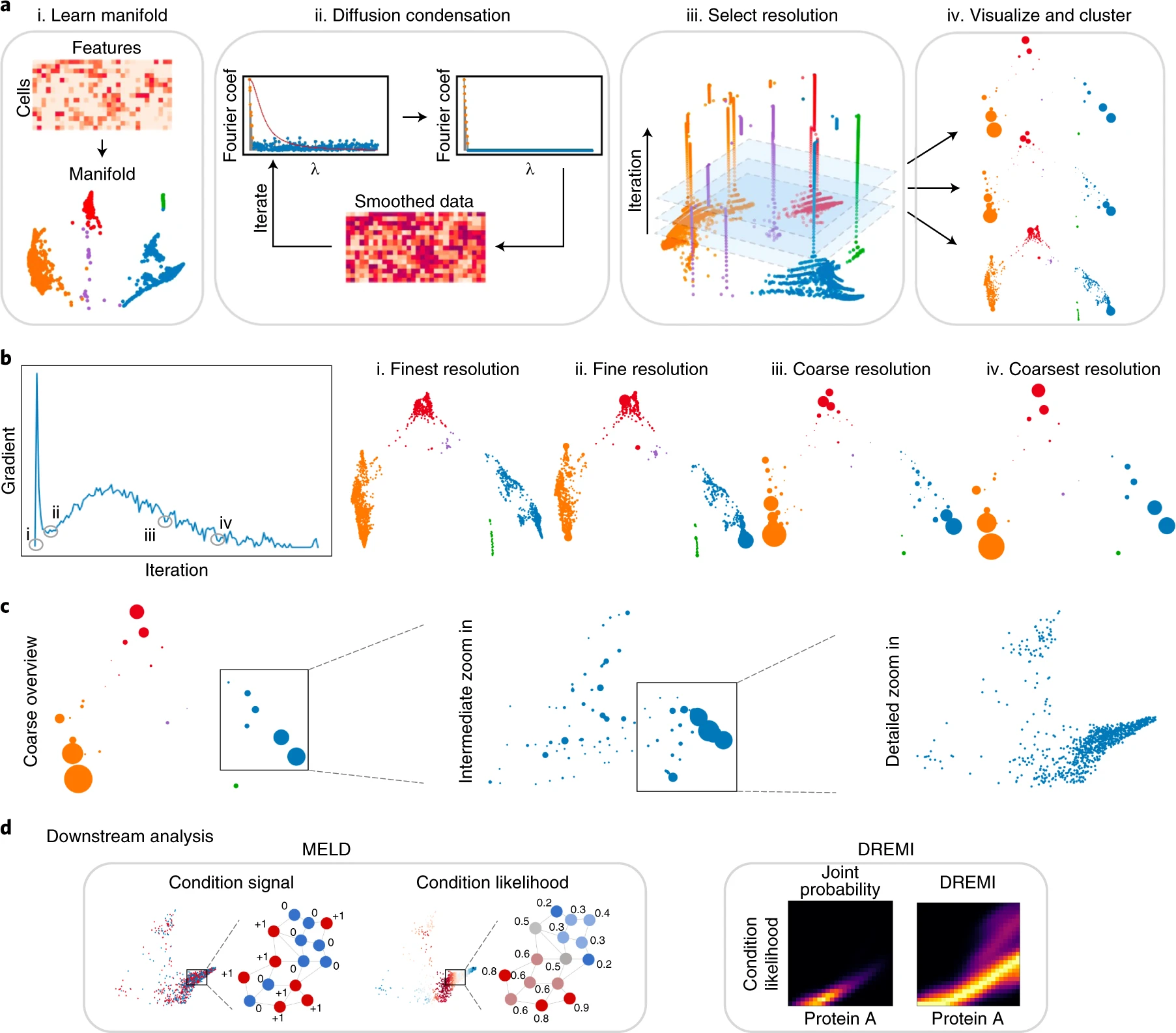
Abstracted biological features across all levels of data granularity
As the biomedical community produces datasets that are increasingly complex and high dimensional, there is a need for more sophisticated computational tools to extract biological insights. We present Multiscale PHATE, a method that sweeps through all levels of data granularity to learn abstracted biological features directly predictive of disease outcome. Built on a coarse-graining process called diffusion condensation, Multiscale PHATE learns a data topology that can be analyzed at coarse resolutions for high-level summarizations of data and at fine resolutions for detailed representations of subsets. We apply Multiscale PHATE to a coronavirus disease 2019 (COVID-19) dataset with 54 million cells from 168 hospitalized patients and find that patients who die show CD16hiCD66blo neutrophil and IFN-γ+ granzyme B+ Th17 cell responses. We also show that population groupings from Multiscale PHATE directly fed into a classifier predict disease outcome more accurately than naive featurizations of the data. Multiscale PHATE is broadly generalizable to different data types, including flow cytometry, single-cell RNA sequencing (scRNA-seq), single-cell sequencing assay for transposase-accessible chromatin (scATAC-seq), and clinical variables.
UDEMD
Fast approximations for earth mover's distance between distributions on a manifold
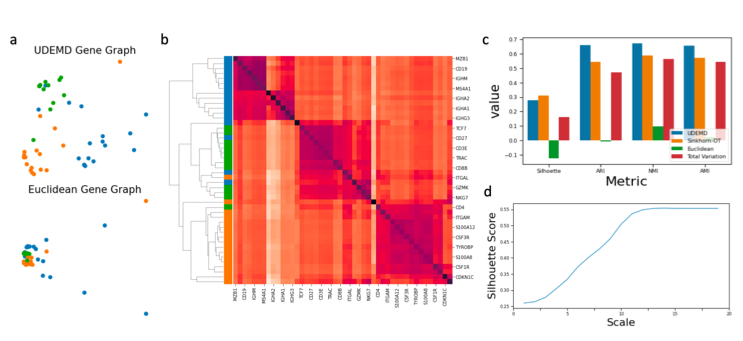
In modern relational machine learning it is common to encounter large graphs that arise via interactions or similarities between observations in many domains. Further, in many cases the target entities for analysis are actually signals on such graphs. We propose to compare and organize such datasets of graph signals by using an earth mover's distance (EMD) with a geodesic cost over the underlying graph. Typically, EMD is computed by optimizing over the cost of transporting one probability distribution to another over an underlying metric space. However, this is inefficient when computing the EMD between many signals. Here, we propose an unbalanced graph earth mover's distance that efficiently embeds the unbalanced EMD on an underlying graph into an L1 space, whose metric we call unbalanced diffusion earth mover's distance (UDEMD). This leads us to an efficient nearest neighbors kernel over many signals defined on a large graph. Next, we show how this gives distances between graph signals that are robust to noise. Finally, we apply this to organizing patients based on clinical notes who are modelled as signals on the SNOMED-CT medical knowledge graph, embedding lymphoblast cells modeled as signals on a gene graph, and organizing genes modeled as signals over a large peripheral blood mononuclear (PBMC) cell graph. In each case, we show that UDEMD-based embeddings find accurate distances that are highly efficient compared to other methods.
MELD
Quantifying the effect of perturbations in single cell RNA-sequencing data
Current methods for comparing single-cell RNA sequencing datasets collected in multiple conditions focus on discrete regions of the transcriptional state space, such as clusters of cells. Here we quantify the effects of perturbations at the single-cell level using a continuous measure of the effect of a perturbation across the transcriptomic space. We describe this space as a manifold and develop a relative likelihood estimate of observing each cell in each of the experimental conditions using graph signal processing. This likelihood estimate can be used to identify cell populations specifically affected by a perturbation. We also develop vertex frequency clustering to extract populations of affected cells at the level of granularity that matches the perturbation response. The accuracy of our algorithm at identifying clusters of cells that are enriched or depleted in each condition is, on average, 57% higher than the next-best-performing algorithm tested. Gene signatures derived from these clusters are more accurate than those of six alternative algorithms in ground truth comparisons.
Integrated Diffusion
multi-modal datasets combined
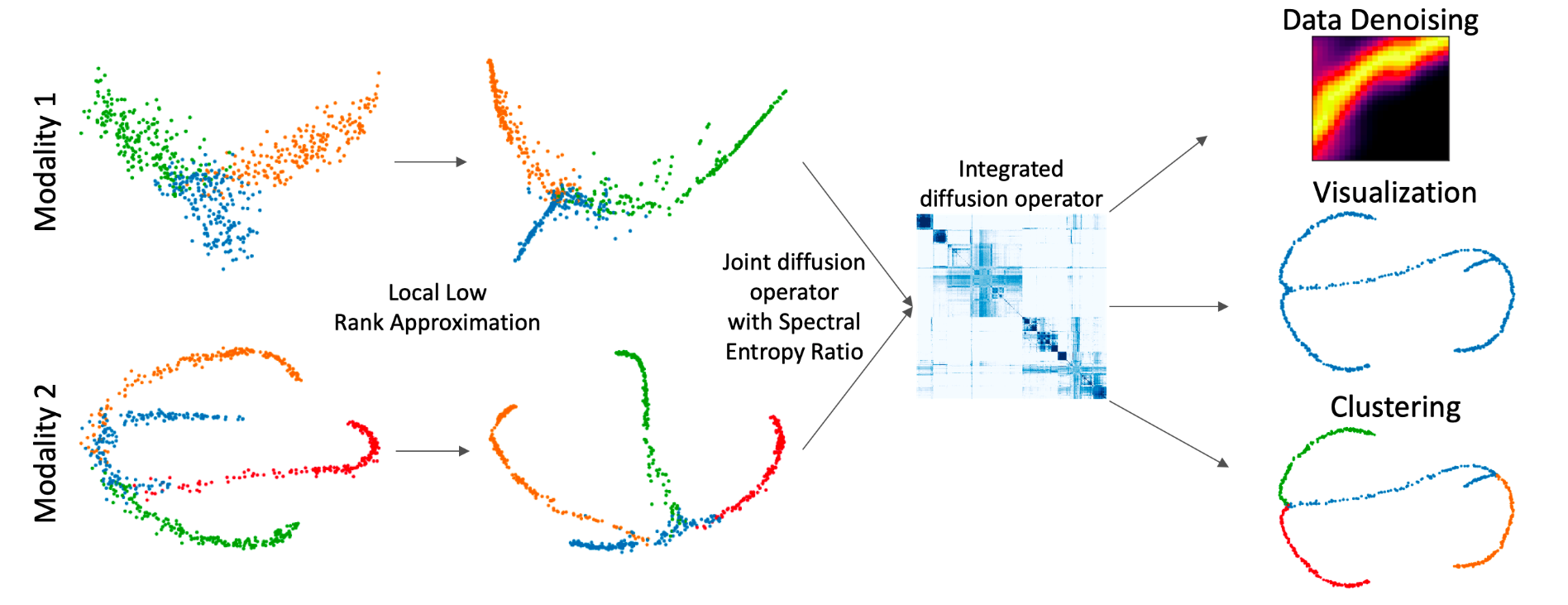
We propose a method called integrated diffusion for combining multimodal data, gathered via different sensors on the same system, to create a integrated data diffusion operator. As real world data suffers from both local and global noise, we introduce mechanisms to optimally calculate a diffusion operator that reflects the combined information in data by maintaining low frequency eigenvectors of each modality both globally and locally. We show the utility of this integrated operator in denoising and visualizing multimodal toy data as well as multi-omic data generated from blood cells, measuring both gene expression and chromatin accessibility. Our approach better visualizes the geometry of the integrated data and captures known cross-modality associations. More generally, integrated diffusion is broadly applicable to multimodal datasets generated by noisy sensors collected in a variety of fields.
DEMD
Fast approximations for earth mover's distance between distributions on a manifold
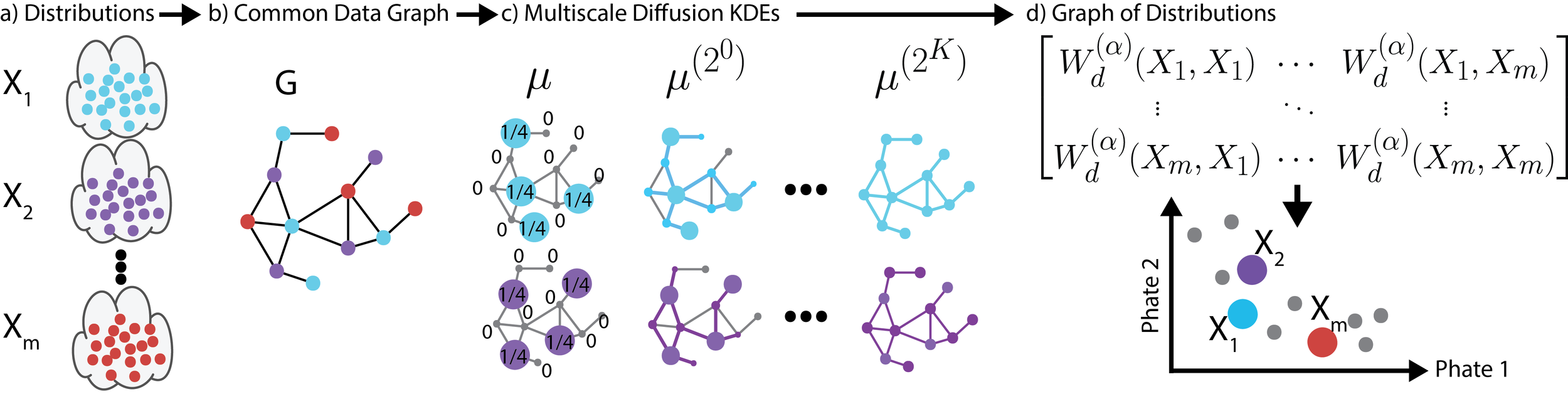
We propose a new fast method of measuring distances between large numbers of related high dimensional datasets called the Diffusion Earth Mover's Distance (EMD). We model the datasets as distributions supported on common data graph that is derived from the affinity matrix computed on the combined data. In such cases where the graph is a discretization of an underlying Riemannian closed manifold, we prove that Diffusion EMD is topologically equivalent to the standard EMD with a geodesic ground distance. Diffusion EMD can be computed in $ ilde{O}(n)$ time and is more accurate than similarly fast algorithms such as tree-based EMDs. We also show Diffusion EMD is fully differentiable, making it amenable to future uses in gradient-descent frameworks such as deep neural networks. Finally, we demonstrate an application of Diffusion EMD to single cell data collected from 210 COVID-19 patient samples at Yale New Haven Hospital. Here, Diffusion EMD can derive distances between patients on the manifold of cells at least two orders of magnitude faster than equally accurate methods. This distance matrix between patients can be embedded into a higher level patient manifold which uncovers structure and heterogeneity in patients. More generally, Diffusion EMD is applicable to all datasets that are massively collected in parallel in many medical and biological systems.

Diffusion EMD
GSAE
Combining the flexibility of deep learning with the represenational power of graph scattering transforms to study thermodynamic landscapes within RNA folding
Biomolecular graph analysis has recently gained much attention in the emerging field of geometric deep learning. Here we focus on organizing biomolecular graphs in ways that expose meaningful relations and variations between them. We propose a geometric scattering autoencoder (GSAE) network for learning such graph embeddings. Our embedding network first extracts rich graph features using the recently proposed geometric scattering transform. Then, it leverages a semi-supervised variational autoencoder to extract a low-dimensional embedding that retains the information in these features that enable prediction of molecular properties as well as characterize graphs. We show that GSAE organizes RNA graphs both by structure and energy, accurately reflecting bistable RNA structures. Also, the model is generative and can sample new folding trajectories.
PhEMD
Single cell analysis of drug perturbations
Previously, the effect of a drug on a cell population was measured based on simple metrics such as cell viability. However, as single-cell technologies are becoming more advanced, drug screen experiments can now be conducted with more complex readouts such as gene expression profiles of individual cells. The increasing complexity of measurements from these multi-sample experiments calls for more sophisticated analytical approaches than are currently available.
We develop a novel method called PhEMD (Phenotypic Earth Mover's Distance) and show that it can be used to embed the space of drug perturbations on the basis of the drugs' effects on cell populations. When testing PhEMD on a newly-generated, 300-sample CyTOF kinase inhibition screen experiment, we find that the state space of the perturbation conditions is surprisingly low-dimensional and that the network of drugs demonstrates manifold structure.
We show that because of the fairly simple manifold geometry of the 300 samples, we can accurately capture the full range of drug effects using a dictionary of only 30 experimental conditions. We also show that new drugs can be added to our PhEMD embedding using similarities inferred from other characterizations of drugs using a technique called Nystrom extension.
Our findings suggest that large-scale drug screens can be conducted by measuring only a small fraction of the drugs using the most expensive high-throughput single-cell technologies -- the effects of other drugs may be inferred by mapping and extending the perturbation space. We additionally show that PhEMD can be useful for analyzing other types of single-cell samples, such as patient tumor biopsies, by mapping the patient state space in a similar way as the drug state space.
We demonstrate that PhEMD is highly scalable, compatible with leading batch effect correction techniques, and generalizable to multiple experimental designs. Altogether, our analyses suggest that PhEMD may facilitate drug discovery efforts and help uncover the network geometry of a collection of single-cell samples.
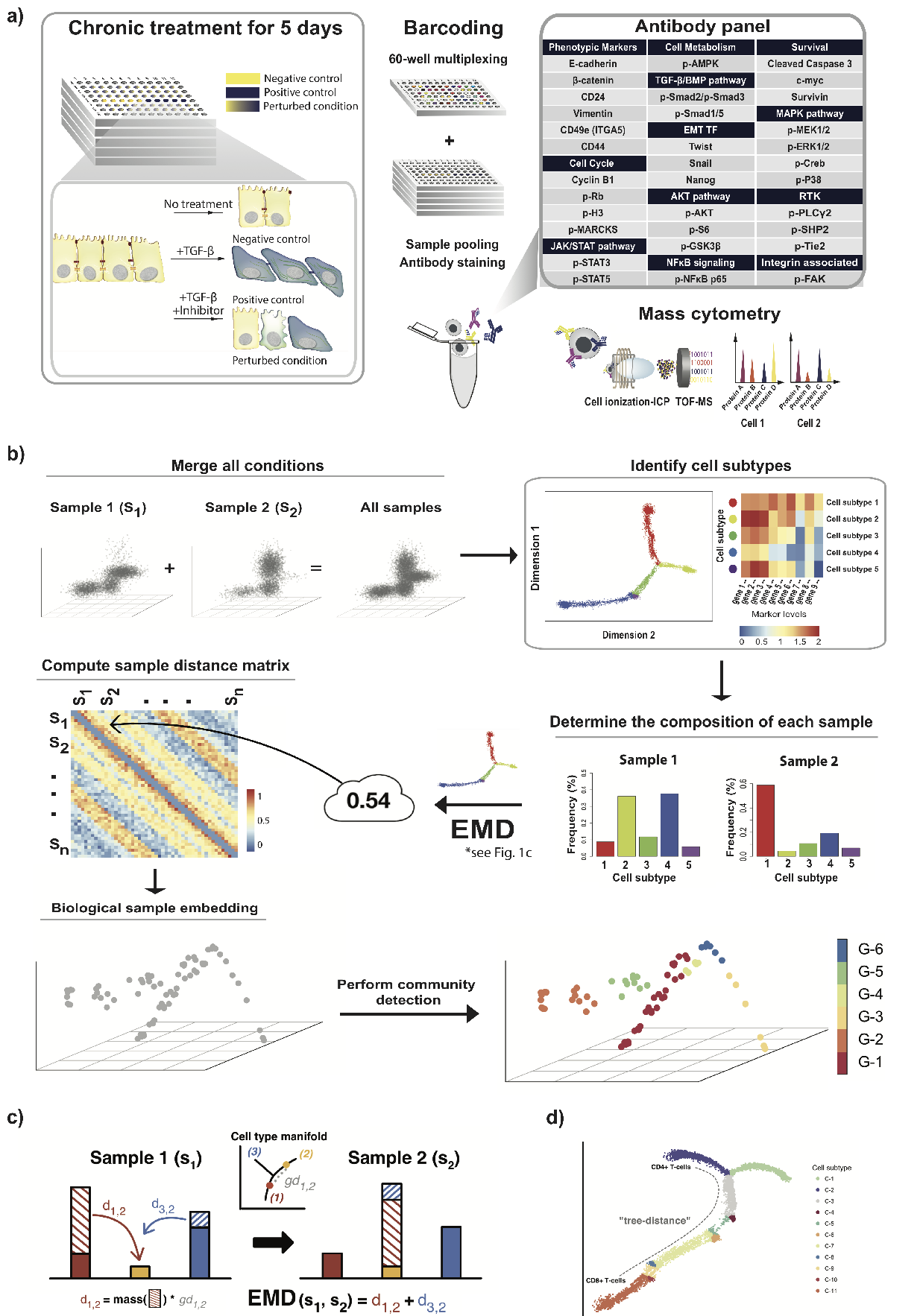
Topological fMRI Analysis
Functional magnetic resonance imaging (fMRI) is a crucial technology for gaining insights into cognitive processes in humans. Data amassed from fMRI measurements result in volumetric data sets that vary over time. However, analysing such data presents a challenge due to the large degree of noise and person-to-person variation in how information is represented in the brain.
To address this challenge, we present a novel topological approach that encodes each time point in an fMRI data set as a persistence diagram of topological features, i.e. high-dimensional voids present in the data. This representation naturally does not rely on voxel-by-voxel correspondence and is robust towards noise. We show that these time-varying persistence diagrams can be clustered to find meaningful groupings between participants, and that they are also useful in studying within-subject brain state trajectories of subjects performing a particular task.
In our preprint, we apply both clustering and trajectory analysis techniques to a group of participants watching the movie 'Partly Cloudy'. We observe significant differences in both brain state trajectories and overall topological activity between adults and children watching the same movie.
See below for an overview of our workflow.
TrajectoryNet
A Dynamic Optimal Transport Network for Modeling Cellular Dynamics
It is increasingly common to encounter data from dynamic processes captured by static cross-sectional measurements over time, particularly in biomedical settings. Recent attempts to model individual trajectories from this data use optimal transport to create pairwise matchings between time points. However, these methods cannot model continuous dynamics and non-linear paths that entities can take in these systems. To address this issue, we establish a link between continuous normalizing flows and dynamic optimal transport, that allows us to model the expected paths of points over time. Continuous normalizing flows are generally under constrained, as they are allowed to take an arbitrary path from the source to the target distribution. We present {TrajectoryNet}, which controls the continuous paths taken between distributions to produce dynamic optimal transport. We show how this is particularly applicable for studying cellular dynamics in data from single-cell RNA sequencing (scRNA-seq) technologies, and that TrajectoryNet improves upon recently proposed static optimal transport-based models that can be used for interpolating cellular distributions.
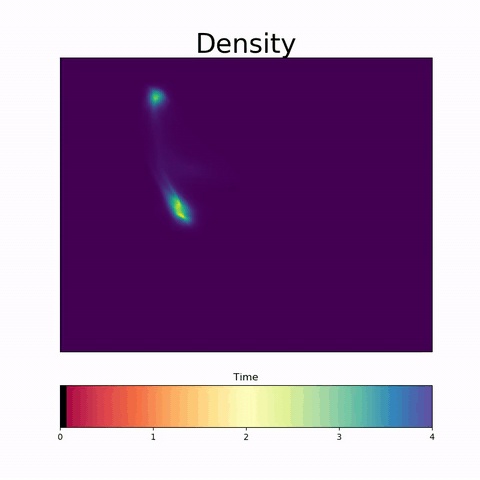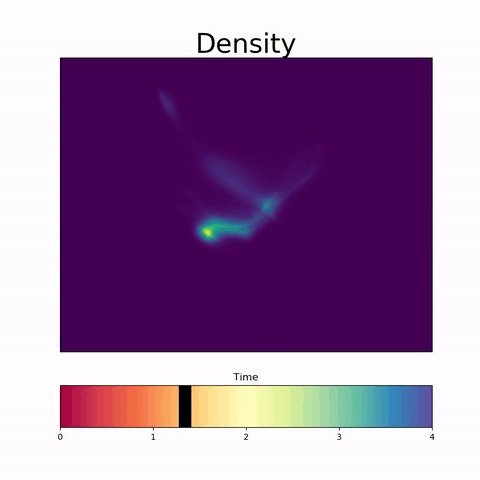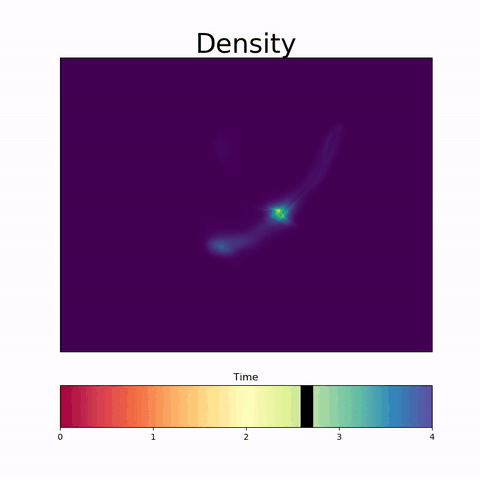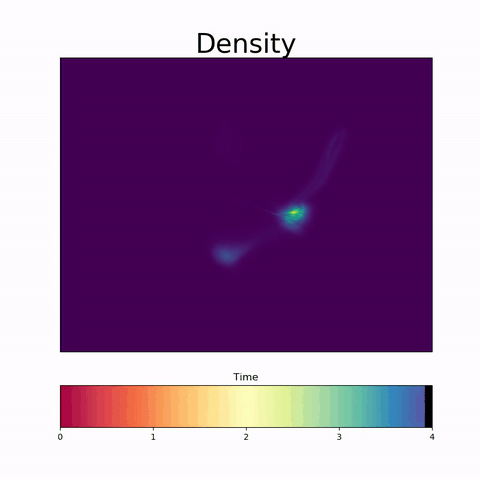

TrajectoryNet: A Dynamic Optimal Transport Network for Modeling Cellular Dynamics
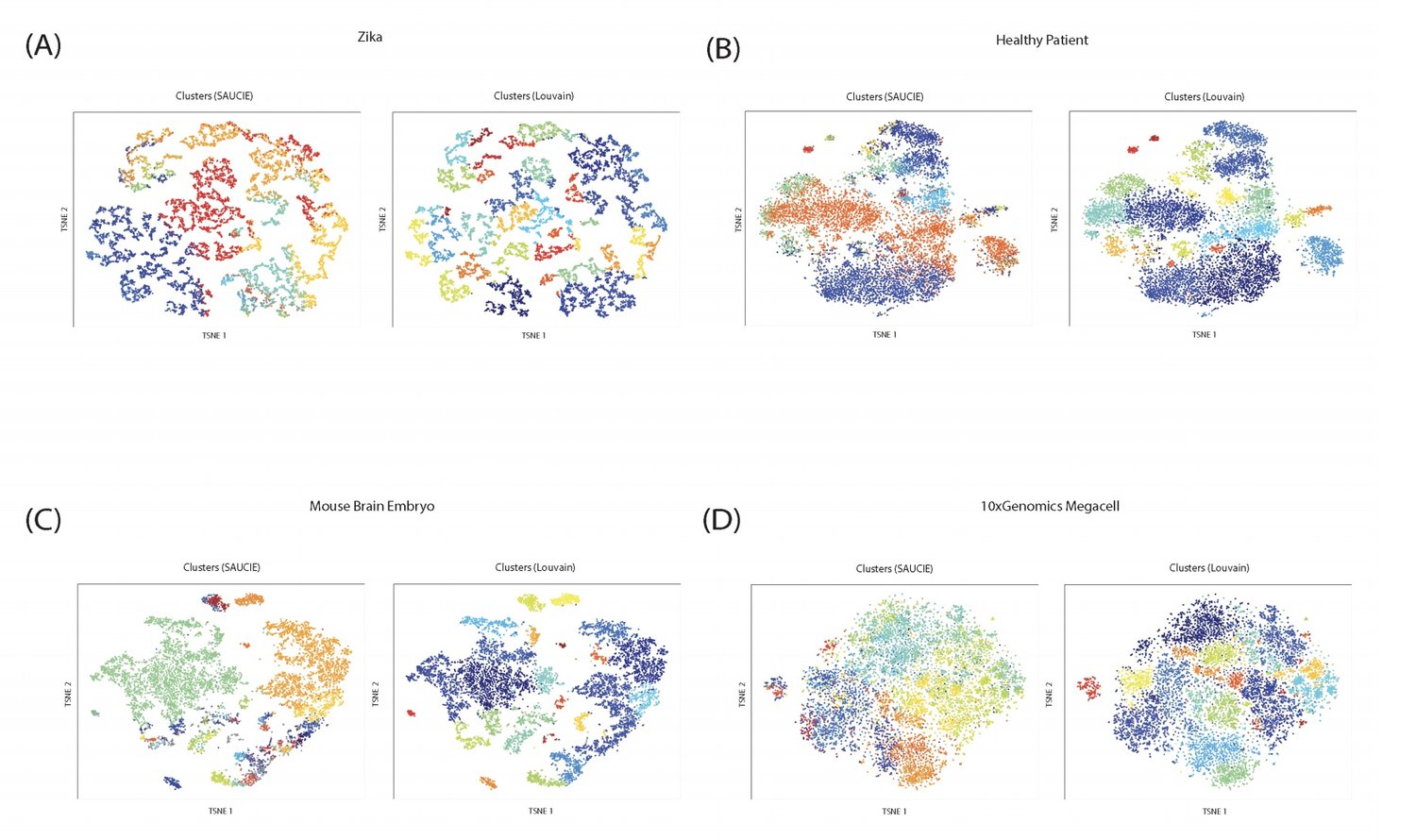
SAUCIE
Exploring Single-Cell Data with Deep Multitasking Neural Networks
Handling the vast amounts of single-cell RNA-sequencing and CyTOF data, which are now being generated in patient cohorts, presents a computational challenge due to the noise, complexity, sparsity and batch effects present. Here, we propose a unified deep neural network-based approach to automatically process and extract structure from these massive datasets.
Our unsupervised architecture, called SAUCIE (Sparse Autoencoder for Unsupervised Clustering, Imputation, and Embedding), simultaneously performs several key tasks for single-cell data analysis including 1) clustering, 2) batch correction, 3) visualization, and 4) denoising/imputation. SAUCIE is trained to recreate its own input after reducing its dimensionality in a 2-D embedding layer which can be used to visualize the data.
Additionally, SAUCIE uses two novel regularizations: (1) an information dimension regularization to penalize entropy as computed on normalized activation values of the layer, and thereby encourage binary-like encodings that are amenable to clustering and (2) a Maximal Mean Discrepancy penalty to correct batch effects. Thus SAUCIE has a single architecture that denoises, batch-corrects, visualizes and clusters data using a unified representation. We show results on artificial data where ground truth is known, as well as mass cytometry data from dengue patients, and single-cell RNA-sequencing data from embryonic mouse brain.
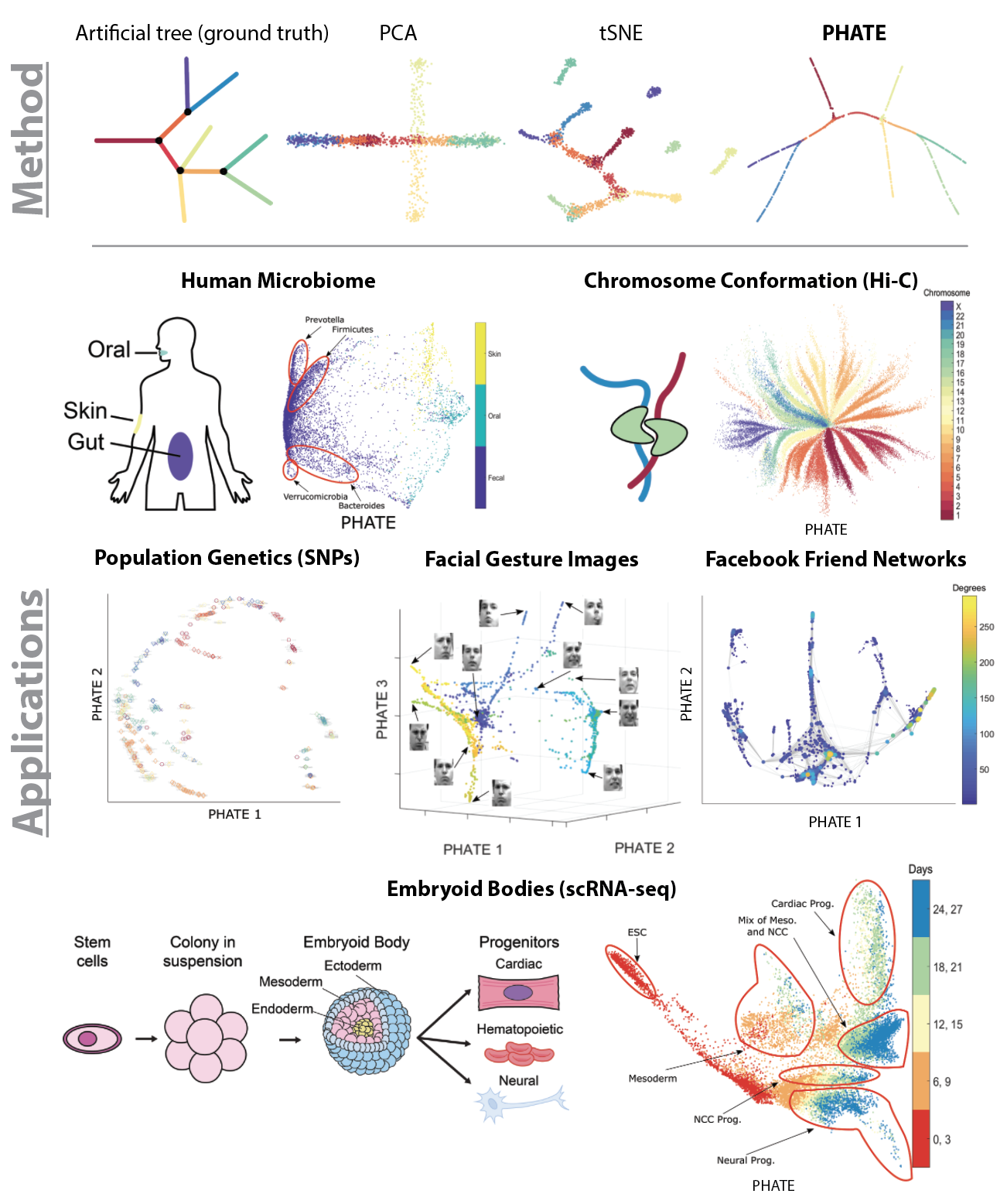
PHATE
Visualizing Transitions and Structure for Biological Data Exploration
In the era of 'Big Data' there is a pressing need for tools that provide human interpretable visualizations of emergent patterns in high-throughput high-dimensional data. Further, to enable insightful data exploration, such visualizations should faithfully capture and emphasize emergent structures and patterns without enforcing prior assumptions on the shape or form of the data.
In this paper, we present PHATE (Potential of Heat-diffusion for Affinity-based Transition Embedding) - an unsupervised low-dimensional embedding for visualization of data that is aimed at solving these issues. Unlike previous methods that are commonly used for visualization, such as PCA and tSNE, PHATE is able to capture and highlight both local and global structure in the data.
MAGAN
Aligning Biological Manifolds
It is increasingly common in many types of natural and physical systems (especially biological systems) to have different types of measurements performed on the same underlying system. In such settings, it is important to align the manifolds arising from each measurement in order to integrate such data and gain an improved picture of the system; we tackle this problem using generative adversarial networks (GANs). Recent attempts to use GANs to find correspondences between sets of samples do not explicitly perform proper alignment of manifolds.
We present the new Manifold Aligning GAN (MAGAN) that aligns two manifolds such that related points in each measurement space are aligned. We demonstrate applications of MAGAN in single-cell biology in integrating two different measurement types together: cells from the same tissue are measured with both genomic (single-cell RNA-sequencing) and proteomic (mass cytometry) technologies. We show that MAGAN successfully aligns manifolds such that known correlations between measured markers are improved compared to other recently proposed models.
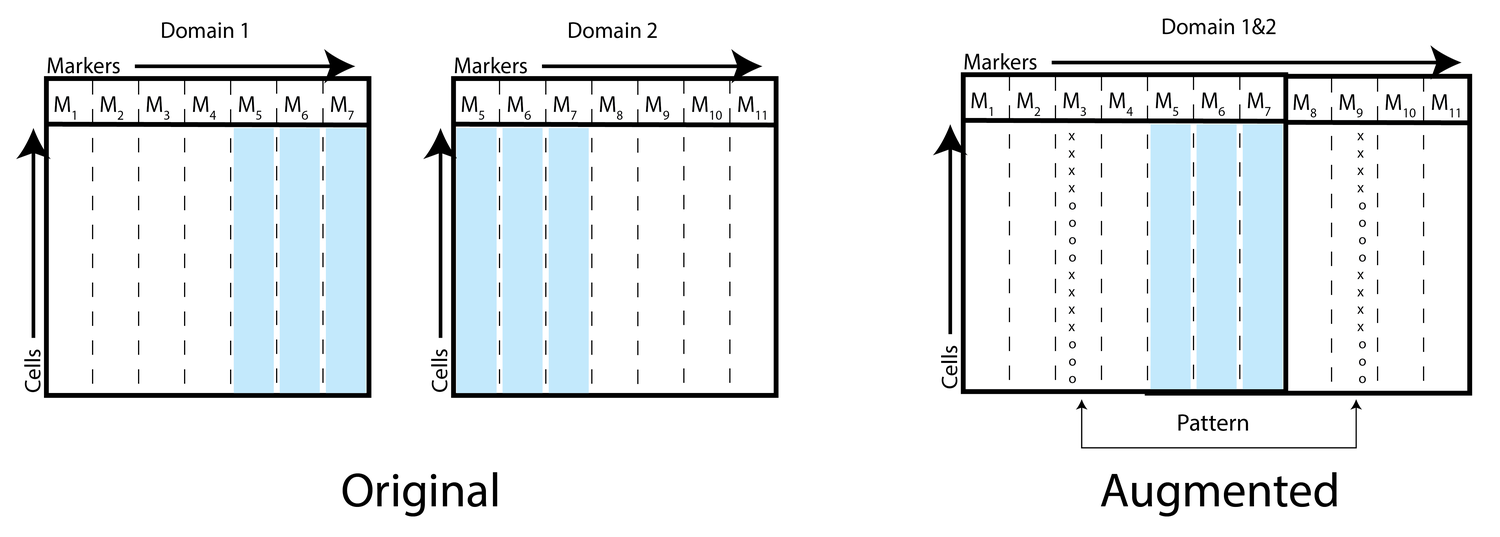
Neuron Editing
Out-of-Sample Extrapolation
While neural networks can be trained to map from one specific dataset to another, they usually do not learn a generalized transformation that can extrapolate accurately outside the space of training. For instance, a generative adversarial network (GAN) exclusively trained to transform images of cars from light to dark might not have the same effect on images of horses. This is because neural networks are good at generation within the manifold of the data that they are trained on. However, generating new samples outside of the manifold or extrapolating "out-of-sample" is a much harder problem that has been less well studied.
To address this, we introduce a technique called neuron editing that learns how neurons encode an edit for a particular transformation in a latent space. We use an autoencoder to decompose the variation within the dataset into activations of different neurons and generate transformed data by defining an editing transformation on those neurons.
By performing the transformation in a latent trained space, we encode fairly complex and non-linear transformations to the data with much simpler distribution shifts to the neuron's activations. We showcase our technique on image domain/style transfer and two biological applications: removal of batch artifacts representing unwanted noise and modeling the effect of drug treatments to predict synergy between drugs.
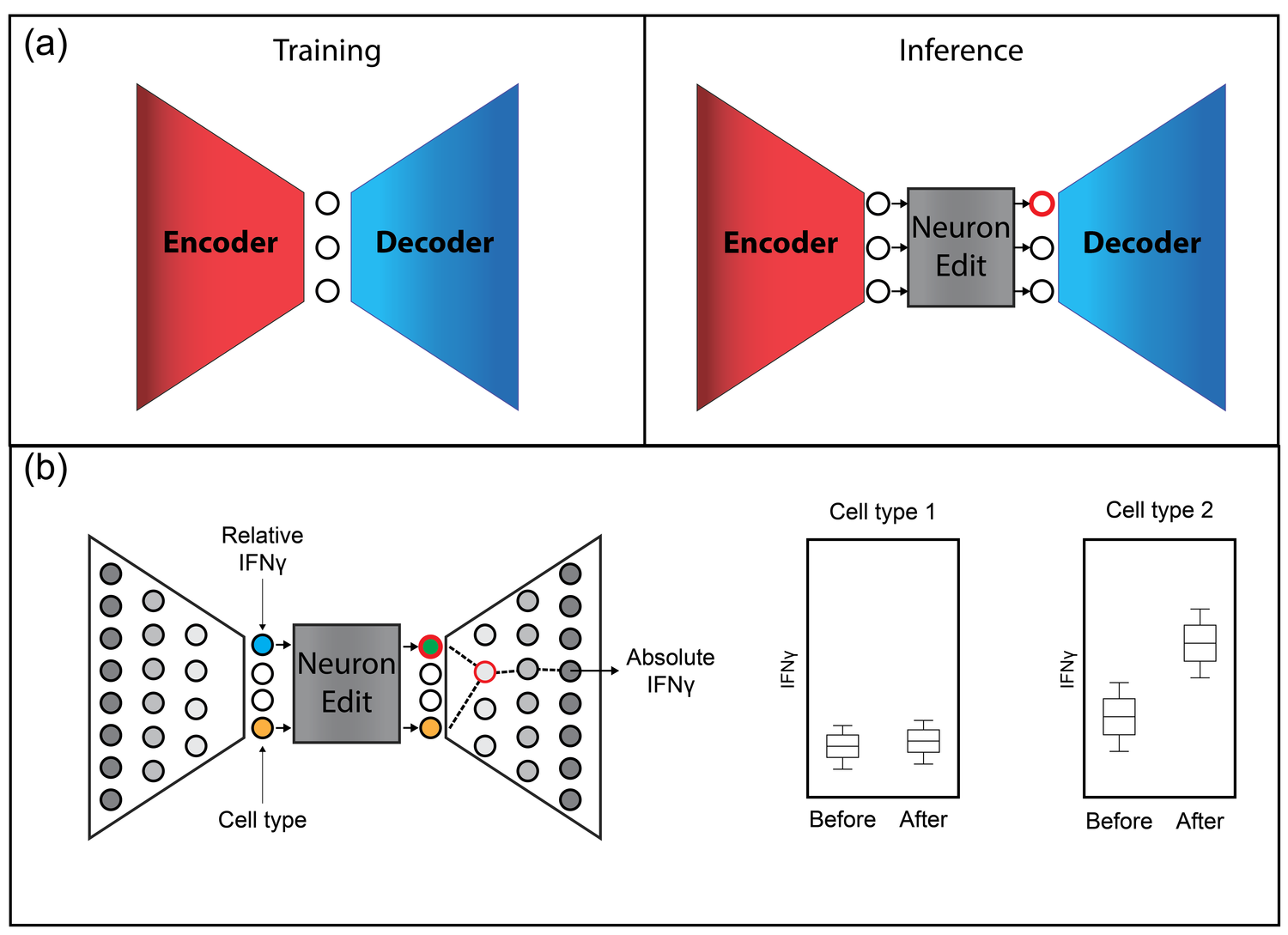
DyMoN
Modeling Dynamics of Biological Systems with Deep Generative Neural Networks
Biological data often contains measurements of dynamic entities such as cells or organisms in various states of progression. However, biological systems are notoriously difficult to describe analytically due to their many interacting components, and in many cases, the technical challenge of taking longitudinal measurements.
This leads to difficulties in studying the features of the dynamics, for examples the drivers of the transition. To address this problem, we present a deep neural network framework we call Dynamics Modeling Network or DyMoN. DyMoN is a neural network framework trained as a deep generative Markov model whose next state is a probability distribution based on the current state.
DyMoN is well-suited to the idiosyncrasies of biological data, including noise, sparsity, and the lack of longitudinal measurements in many types of systems. Thus, DyMoN can be trained using probability distributions derived from the data in any way, such as trajectories derived via dimensionality reduction methods, and does not require longitudinal measurements.
We show the advantage of learning deep models over shallow models such as Kalman filters and hidden Markov models that do not learn representations of the data, both in terms of learning embeddings of the data and also in terms training efficiency, accuracy and ability to multitask. We perform three case studies of applying DyMoN to different types of biological systems and extracting features of the dynamics in each case by examining the learned model.
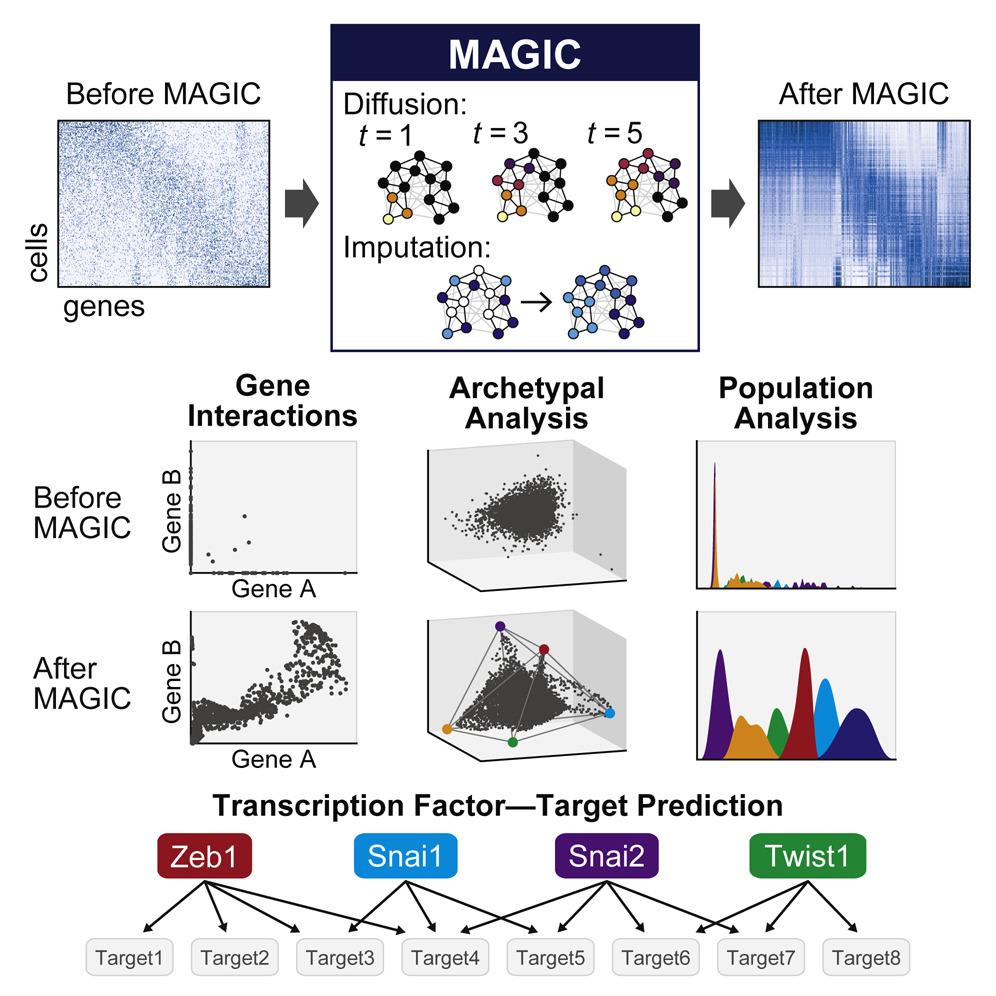
MAGIC
Recovering Gene Interactions from Single-Cell Data Using Data Diffusion
Single-cell RNA-sequencing is fast becoming a major technology that is revolutionizing biological discovery in fields such as development, immunology and cancer. The ability to simultaneously measure thousands of genes at single cell resolution allows, among other prospects, for the possibility of learning gene regulatory networks at large scales. However, scRNA-seq technologies suffer from many sources of significant technical noise, the most prominent of which is dropout due to inefficient mRNA capture. This results in data that has a high degree of sparsity, with typically only 10% non-zero values.
To address this, we developed MAGIC (Markov Affinity-based Graph Imputation of Cells), a method for imputing missing values, and restoring the structure of the data. After MAGIC, we find that two- and three-dimensional gene interactions are restored and that MAGIC is able to impute complex and non-linear shapes of interactions. MAGIC also retains cluster structure, enhances cluster-specific gene interactions and restores trajectories, as demonstrated in mouse retinal bipolar cells, hematopoiesis, and our newly generated epithelial-to-mesenchymal transition dataset.
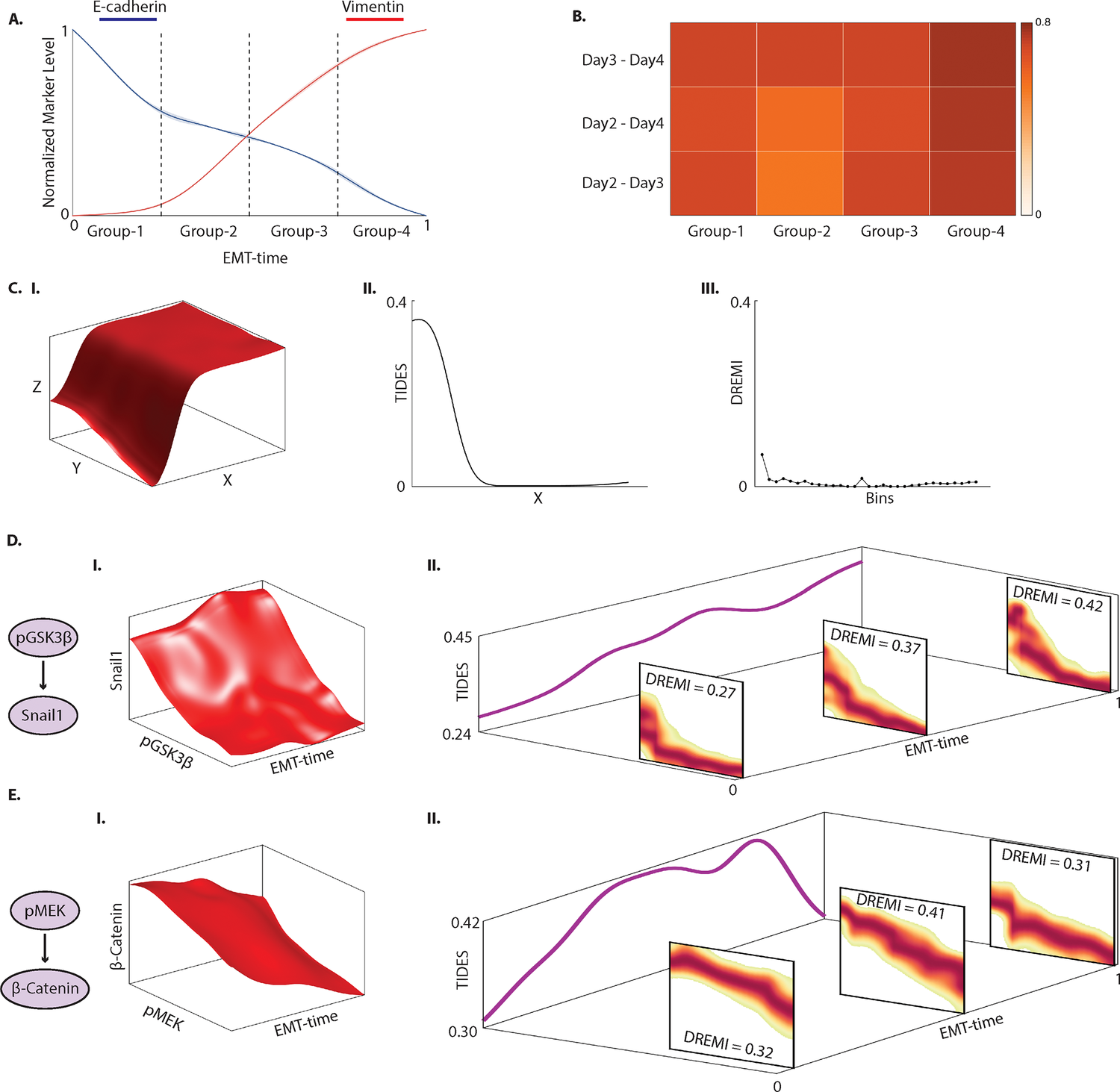
TIDES
TIDES or ( Trajectory Interpolated DREMI Scores) is an extension of our earlier Density Resampled Estimate of Mutual Information which quantifies time-varying edge behavior over a developmental trajectory. In particular it tracks times during development in which a regulatory relationship is strong (high mutual information) vs times when regulatory relationships are inactive (low mutual information) due to regulatory network rewiring that underlies differentiation. We also predict an overall metric of edge dynamism, which combined with TIDES allows us to predict the effect of drug perturbations on the Epithelial-to-Mesenchymal transition in breast cancer cells.
SUGAR
Geometry-Based Data Generation
Many generative models attempt to replicate the density of their input data. However, this approach is often undesirable, since data density is highly affected by sampling biases, noise, and artifacts. We propose a method called SUGAR (Synthesis Using Geometrically Aligned Random-walks) that uses a diffusion process to learn a manifold geometry from the data. Then, it generates new points evenly along the manifold by pulling randomly generated points into its intrinsic structure using a diffusion kernel.
SUGAR equalizes the density along the manifold by selectively generating points in sparse areas of the manifold. We demonstrate how the approach corrects sampling biases and artifacts, while also revealing intrinsic patterns (e.g. progression) and relations in the data. The method is applicable for correcting missing data, finding hypothetical data points, and learning relationships between data features.
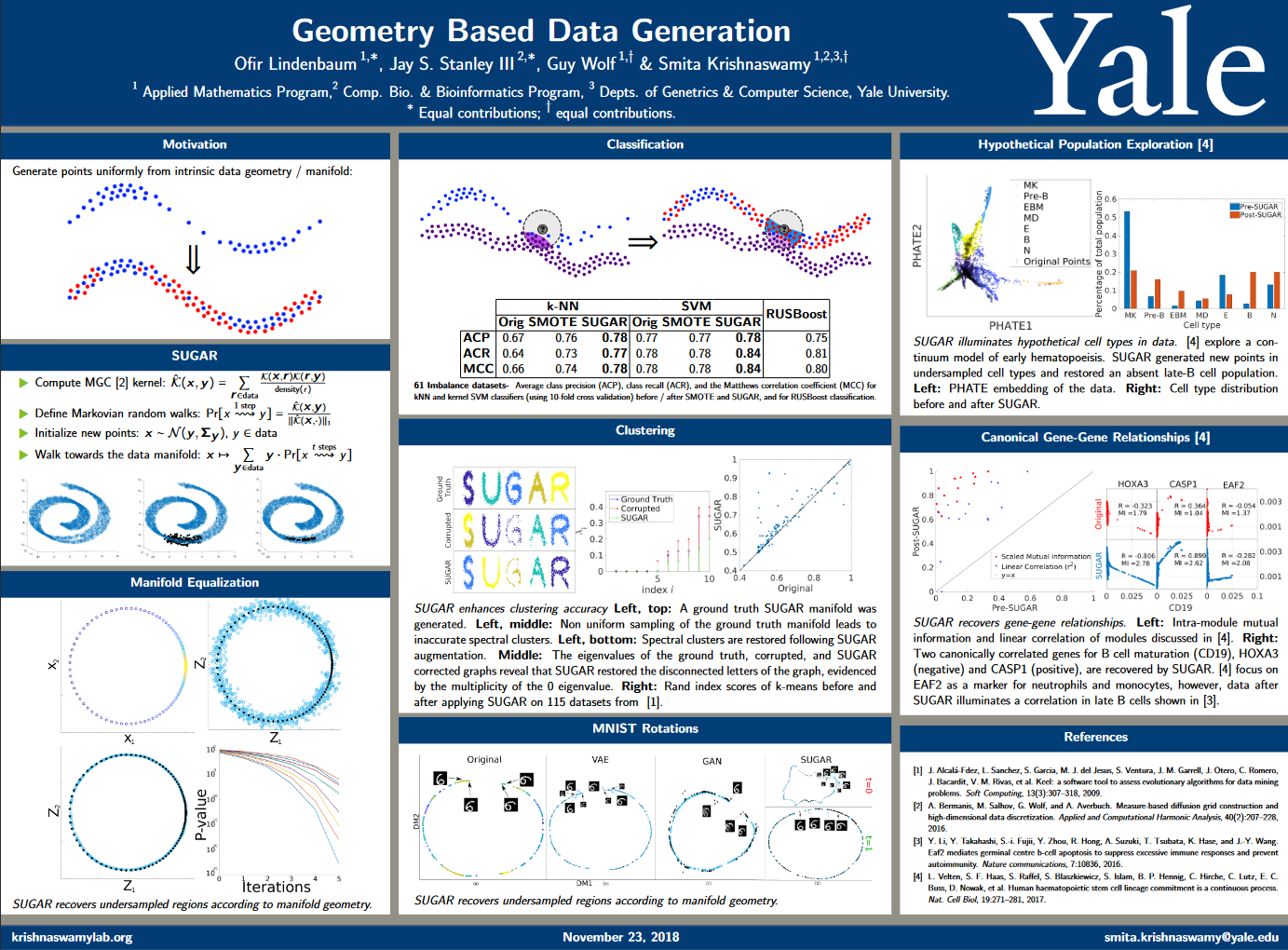

Geometry Based Data Generation
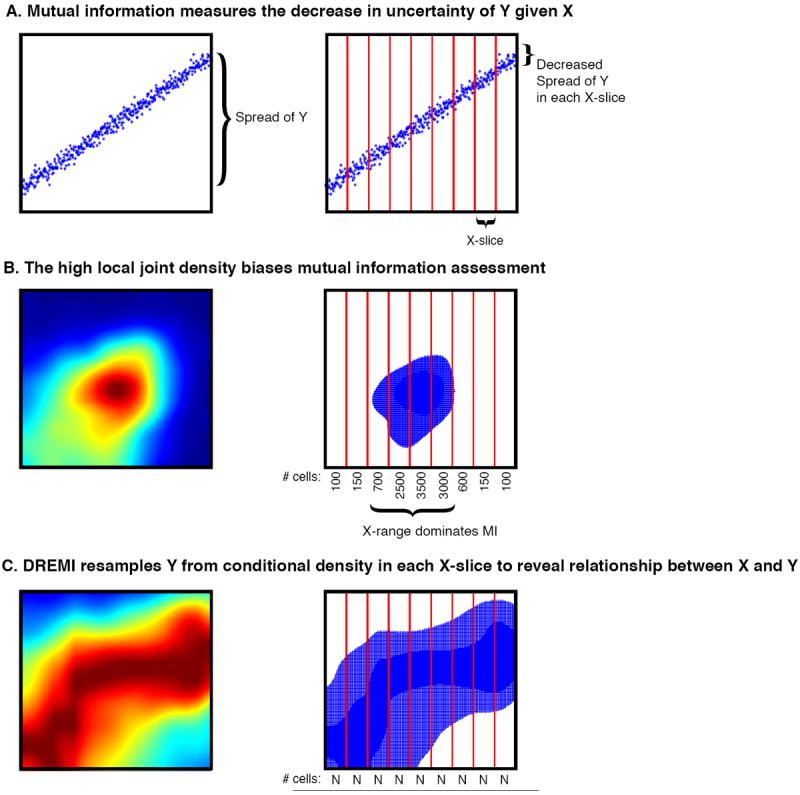
DREMI
Learning time-varying information flow from single-cell EMT data
Cellular circuits sense the environment, process signals, and compute decisions using networks of interacting proteins. To model such a system, the abundance of each activated protein species can be described as a stochastic function of the abundance of other proteins. High-dimensional single-cell technologies, like mass cytometry, offer an opportunity to characterize signaling circuit-wide. However, the challenge of developing and applying computational approaches to interpret such complex data remains.
Here, we developed computational methods, based on established statistical concepts, to characterize signaling network relationships by quantifying the strengths of network edges and deriving signaling response functions. In comparing signaling between naïve and antigen-exposed CD4+ T-lymphocytes, we find that although these two cell subtypes had similarly-wired networks, naïve cells transmitted more information along a key signaling cascade than did antigen-exposed cells.
We validated our characterization on mice lacking the extracellular-regulated MAP kinase (ERK2), which showed stronger influence of pERK on pS6 (phosphorylated-ribosomal protein S6), in naïve cells compared to antigen-exposed cells, as predicted. We demonstrate that by using cell-to-cell variation inherent in single cell data, we can algorithmically derive response functions underlying molecular circuits and drive the understanding of how cells process signals.