DEMD

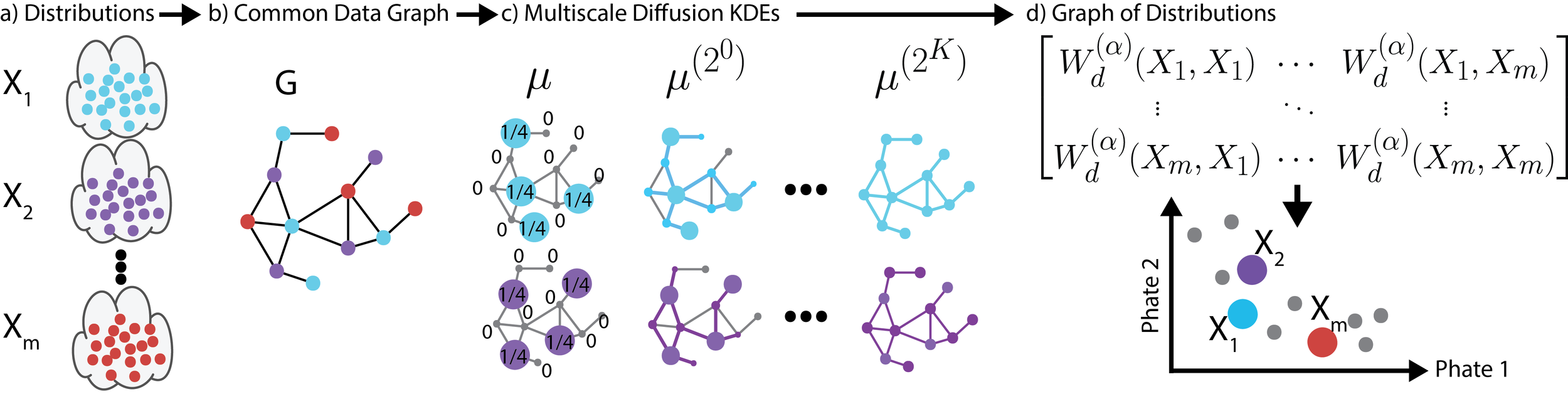
We propose a new fast method of measuring distances between large numbers of related high dimensional datasets called the Diffusion Earth Mover's Distance (EMD). We model the datasets as distributions supported on common data graph that is derived from the affinity matrix computed on the combined data. In such cases where the graph is a discretization of an underlying Riemannian closed manifold, we prove that Diffusion EMD is topologically equivalent to the standard EMD with a geodesic ground distance. Diffusion EMD can be computed in $ ilde{O}(n)$ time and is more accurate than similarly fast algorithms such as tree-based EMDs. We also show Diffusion EMD is fully differentiable, making it amenable to future uses in gradient-descent frameworks such as deep neural networks. Finally, we demonstrate an application of Diffusion EMD to single cell data collected from 210 COVID-19 patient samples at Yale New Haven Hospital. Here, Diffusion EMD can derive distances between patients on the manifold of cells at least two orders of magnitude faster than equally accurate methods. This distance matrix between patients can be embedded into a higher level patient manifold which uncovers structure and heterogeneity in patients. More generally, Diffusion EMD is applicable to all datasets that are massively collected in parallel in many medical and biological systems.