MIOFlow

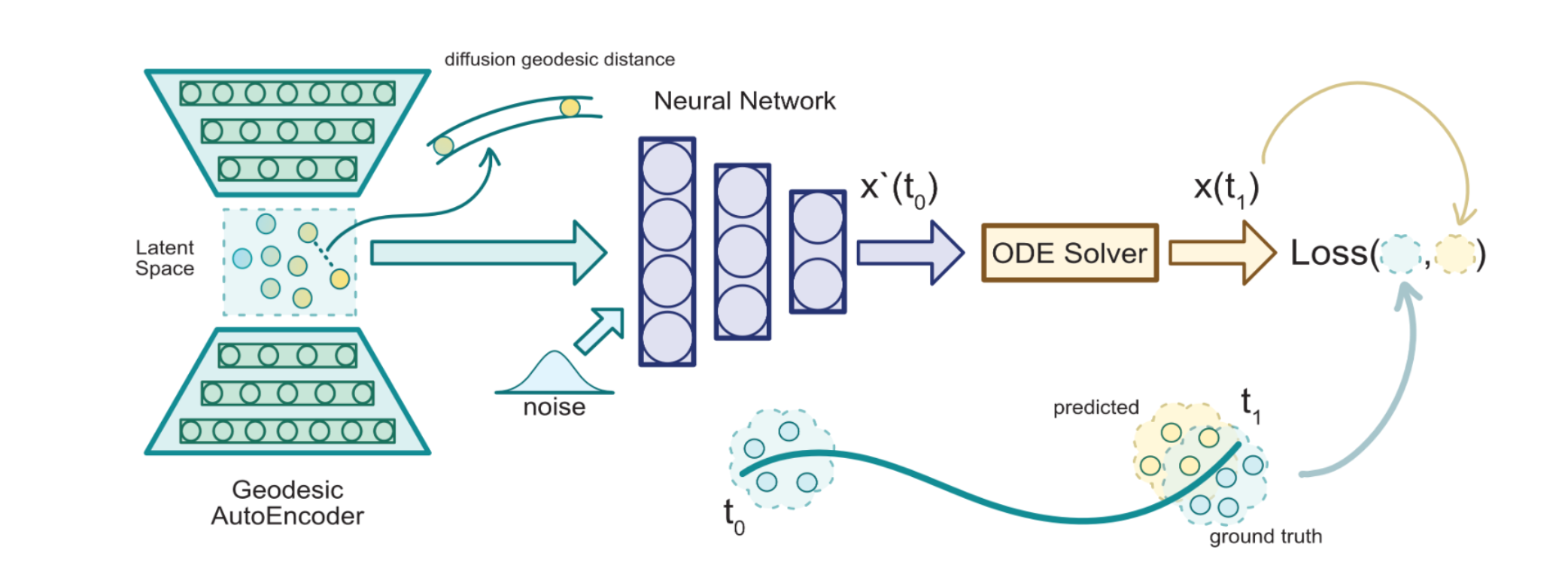
We present a method called Manifold Interpolating Optimal-Transport Flow (MIOFlow) that learns stochastic, continuous population dynamics from static snapshot samples taken at sporadic timepoints. MIOFlow combines dynamic models, manifold learning, and optimal transport by training neural ordinary differential equations (Neural ODE) to interpolate between static population snapshots as penalized by optimal transport with manifold ground distance. Further, we ensure that the flow follows the geometry by operating in the latent space of an autoencoder that we call a geodesic autoencoder (GAE). In GAE the latent space distance between points is regularized to match a novel multiscale geodesic distance on the data manifold that we define. We show that this method is superior to normalizing flows, Schrödinger bridges and other generative models that are designed to flow from noise to data in terms of interpolating between populations. Theoretically, we link these trajectories with dynamic optimal transport. We evaluate our method on simulated data with bifurcations and merges, as well as scRNA-seq data from embryoid body differentiation, and acute myeloid leukemia treatment.